Préambule
De par leur aspect purement esthétique, les fractales ont longtemps été considérées par les mathématiciens comme sans intérêt pour
des applications concrètes aux mathématiques. Ce n'est qu'à partir de la parution du livre Les Objets fractals - Forme, hasard et dimension
écrit en 1974 par Mandelbrot que le grand public prend conscience du potentiel que représente les fractales.
Cette section présente les applications les plus courantes des fractales.
L'art fractal
C'est une forme d'application qui consiste à produire toute forme d'art à partir de fractales. L'art fractal s'applique à des domaines divers et variés comme les images, des animations et même de la musique ! L'art fractal est généralement crée à partir d'un ordinateur où l'utilisateur rentre divers paramètres afin de contrôler la génération de la fractale.
Types
Les fractales apparentées à l'art fractal peuvent être divisées en différents groupes, ou catégories. Voici les plus connues :
- Les fractales dérivées de la géomètrie (flocon de Koch, tapis de Sierpinski, ...)
- Les ensembles de fractales (ensemble de Mandelbrot)
- Les systèmes de fonctions itérées
- Les systèmes de fractales appartenant au L-systeme (plantes fractales)
- Les fractales 3D (Mandelbulb, Mandelbox, ...)
- Et bien d'autres encore : Voir plus

Exemples

Fractales dans les films
Certians artistes utilisent les fractales afin de réaliser des environnements 3D dans les films. C'est le cas de Hal Tenny qui a réalisé la planète du film Les Gardiens de la Galaxie à l'aide du logiciel Mandelbulb.
En savoir plus
Fractales dans la peinture
Des artistes utilisent également les fractales dans la peinture afin de reproduire fidélement des éléments naturelles. Le peintre Hokusai s'en ait servi pour réaliser son tableau La Grande Vague de Kawagana.
En savoir plus
Fractales appliquées aux maths
Un aspect également plus théorique des fractales peut s'appliquer aux mathématiques comme cette repésentation fractales du mot de Fibonacci (Opération de concaténation ce que les nombres de Fibonacci sont à l'addition).
En savoir plusBiologie/Géologie
Il semblerait que les fractales soient au coeur de la nature. D'après Mandelbrot, ces dernières permettrait de décrire des phénomènes naturels qui étaient alors inexplicables comme la formation des chaines de montagne, les ramifications des arbres, la forme des nuages, etc...
Un modèle pour la loi entre le rapport masse/consommation d'energie les êtres vivants
Les chercheurs britanniques Geoffrey B. West, James H. Brown et Brian J. Enquist ont étudié ce sujet et découvert que le mystère réside dans les fractales. Aujourd'hui leurs recherches visent à determiner si la structure fractale d'un arbre peut renseigner sur le comportement d'une forêt entière. D'après leurs recherches préliminaires il semblerait qu'il y ait un lien évident entre le nombre et la taille des branches d'un arbre et l'effectif des arbres dans une forêt ainsi que leur taille. En savoir plusInformatique
Dans l'informatique de nombreux logiciels permettant de visualiser/créer des fractales. Citons parmis les plus répandus :
- En 2D
- Xaos
- Electric Sheep
- Fractint
- En 3D
- Mandelbulb3D
- Mandelbulber
- Gaston
De nombreux autres programmes permettent égalment de créer des fractales même si ce n'est pas leur fonction première. Ainsi tout logiciel qui permet de créer des objets à partir d'un language de programmation peut servir à la création de fractals. Les principaux pour la modélisation 3D : Blender (Python), FreeCAD (Python) et Autocad (LISP). Pour la 2D, Illustrator propose des outils de fractalisation.
Pour ce qui est du Hardware, la découverte des fractales à permis la miniaturisation et une meilleure réception des antennes. Les fractales qui peuvent avoir une dimension infinie pour une même longueur permettent ainsi à nos smartphone de recevoir et emettre des ondes de longueur d'ondes différents (WiFi, Bluetooth, Réseau, NFC,..) tout en étant compact.
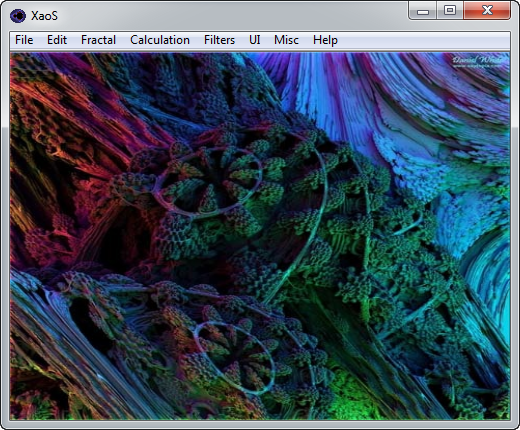
Isolation sonore
Dans l'isolation sonore, les fractales ont encore une fois leur utilité. En effet Il suffit de répéter sur une surface un motif fractal simple (en relief bien sûr), qui augmentera ainsi la surface de contact avec l'onde. Comme cette surface est brisée l'onde sera très peu réfléchie par le mur.
A une fréquence de 250 Hz, un mur "fractal" ne renvoie que 15% de l'intensité sonore, alors qu'un mur classique en renvoie 45%. De plus la réflexion des ondes sonores est diminuée de 8 dB, tandis que la transmission (la capacité des sons à trasverser les murs) est réduite de 57 dB. Ceci représente une absorbtion 4 fois plus importante que les autres murs antibruit.
Malgré la simplicité du motif, le moulage de telles formes n'est pas facile, en résulte un coût de facrication plus important que pour un mur classique. Bien que le prix soit plus élevé, ces murs fractals devraient trouver une application pour insonoriser les habitations proches des grands axes routiers.

