Historique
Benoît Mandelbrot était un mathématicien franco-américain du 20e siècle à qui l'on a attribué la découverte de nouveaux objects mathématiques : les fractales. En 1967 il prend comme exemple la longueur de la côte de la Grande-Bretagne, afin de définir une nouvelle forme de hasard. Selon lui, la longueur dépend de l’échelle à laquelle on la mesure, et possède une dimension de Hausdorff non entière, comprise entre 1 et 2, et c’est en acceptant cette idée de dimension non entière qu'il met en évidence pour la première fois la théorie des fractales.
Il inventa le mot "Fractale" en 1975 qui permet de mettre on nom sur tous les "monstres" naient des mathématiques durant les 2 siècles précédents (comme les ensembles de Julia). Des objets qui sont beaucoup trop irréguliés pour être analysé par la géométrie classique. Cela regroupe les objets auto-similaires où l'image se retrouve a l'identique a toute échelles et les objets qui manques de régularité (comme les courbes de la bourse par exemple).
Il donnera même son nom a une famille de fractales : L'ensemble de Mandelbrot, que nous allons vous présenter sur cette page. Il a également montré qu'un grand nombre d’objets dans la nature pouvaient être décrits par des fractales, conduisant ainsi à de nouveaux terrains de recherche.
Ensemble de julia
Les ensembles de Julia sont des ensembles de points d'un plan tel que lorsque l'on applique successivement une formule du type \(z_n^2+c\) a un point, la suite engendrée par ce point est convergente, c'est a dire qu'il engendre une suite bornée.
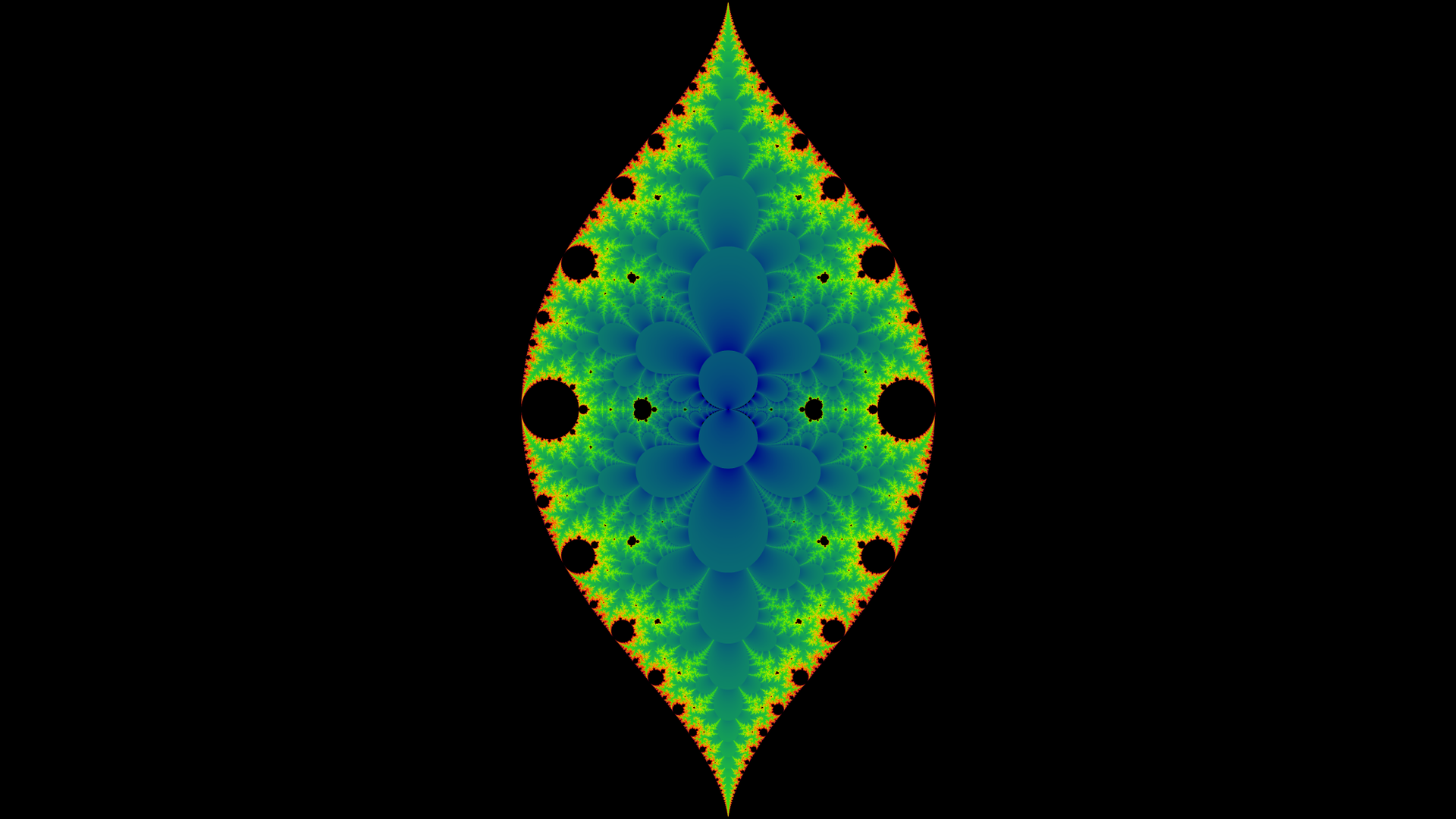
On peut classer les ensembles de Julia dans 2 catégories : Les ensembles connexes, et les ensemble non-connexes. Un ensemble connexe est un ensemble dont la représentation est constitué d'un seul block comme l'image ci-contre.
Pour représenter un ensemble de Julia on peut colorer en noir les points qui engendrent une suite convergente, et en blanc, ceux qui engendre une suite divergente.
Vous pouvez observer a droite la représentation de l'ensemble de Julia de formule \(z_n^2-3/4\).
Définition
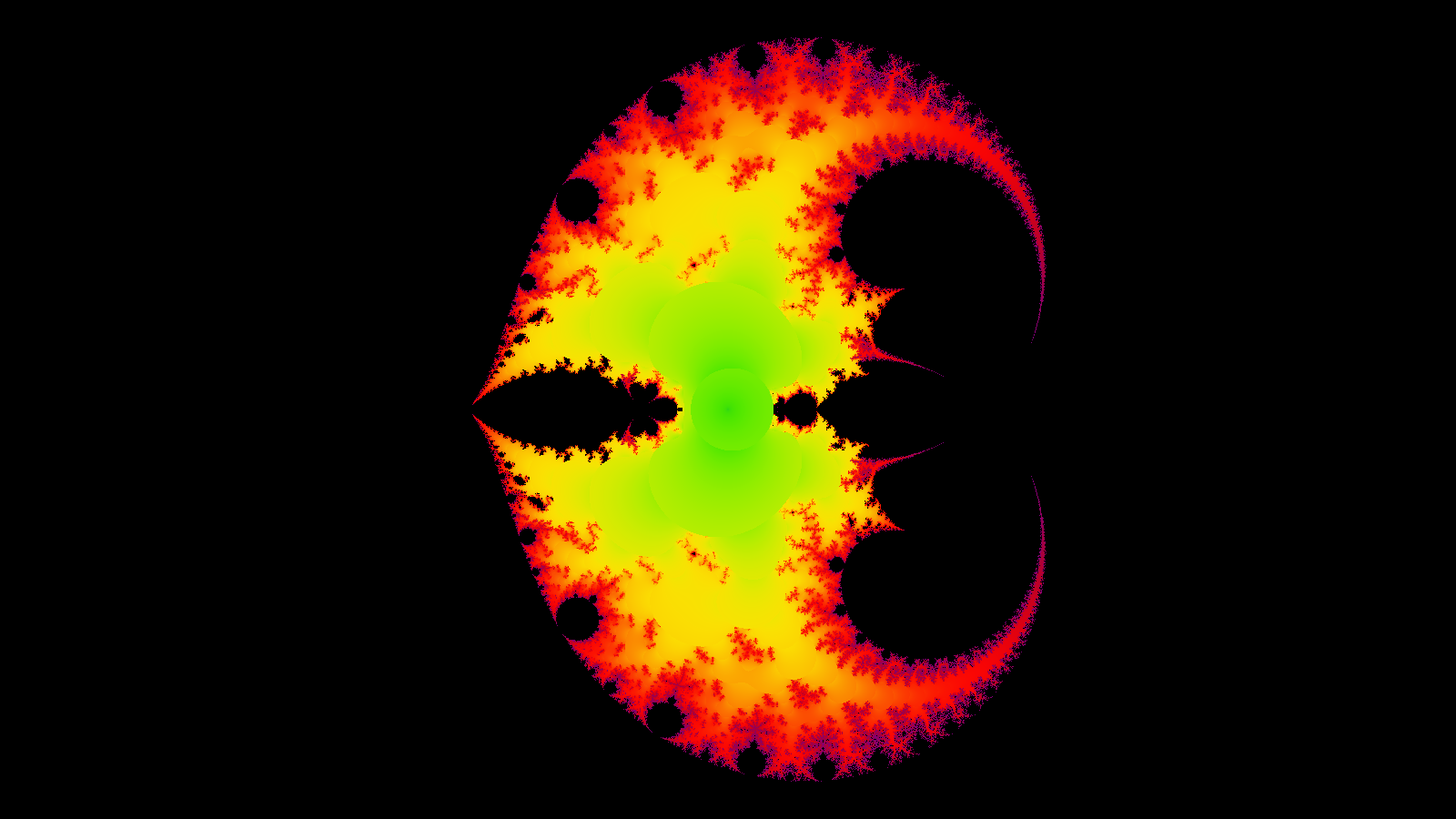
L'ensemble de Mandelbrot est une fractale définie comme l'ensemble des points c du plan complexe pour lesquels la suite de nombres complexes est définie par la récurrence suivante :
\(z_{n+1}=Z_n^2+c\)
Avec \(z_n\) et c des nombres complexes.
Chaque point de l'ensemble correspond alors a un ensemble de Julia. On a donc \(c = x + i*y\).
On peut le caractériser de Carte des ensembles de Julia.
La dimension de Hausdorff de la frontière de l'ensemble de Mandelbrot vaut 2. Cela a été démontré en 1990 par Mitsuhiro Shishikura.
Autosimilarité
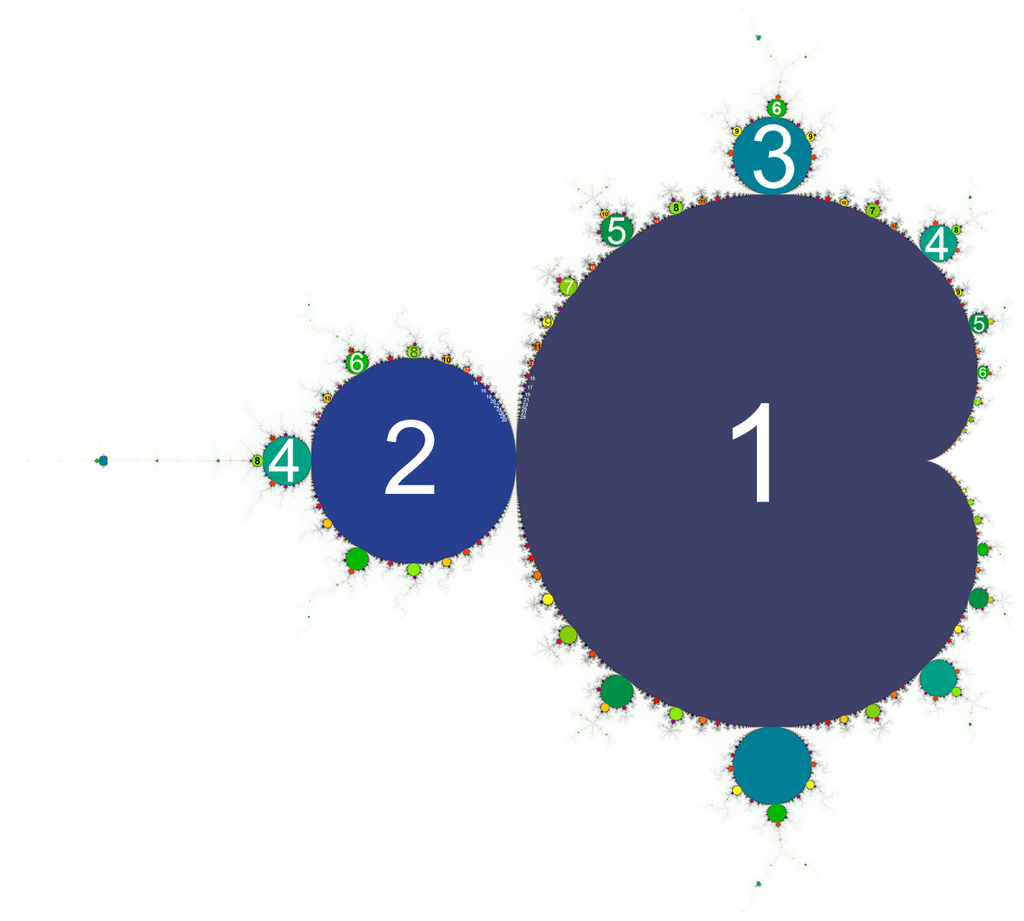
L'ensemble de Mandelbrot est autosimilaire dans le voisinage des points de Misiurewicz. Des versions réduites de l'ensemble de Mandelbrot apparaissent sur toute sa frontière, jusqu'à des grossissements infinis, avec de légères différences. Cependant, de manière générale, l'ensemble de Mandelbrot n'est pas, strictement autosimilaire, c'est a dire que pour la quasi totalité des autres points, on ne retrouvera pas de motifs similaire lors d'un zoom sur ces derniers.
Bourgeons, antennes et périodicités
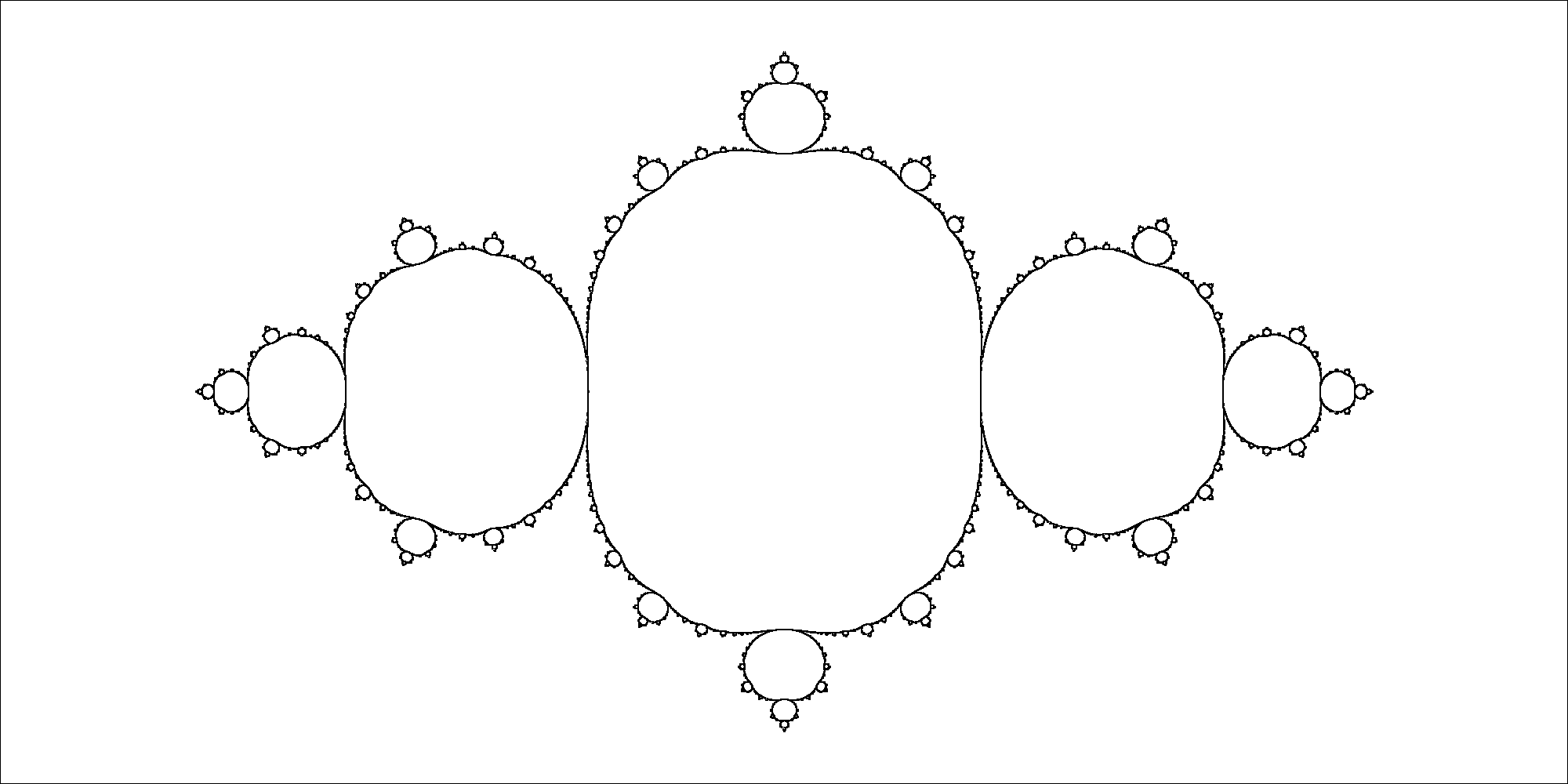
L'ensemble de Mandelbrot fait apparaître nombre de structures en forme de bourgeons entourant une structure principale en forme de cartoïde.
- La cardioïde est l'ensemble des points c qui convergent vers un point fixe : période 1.
- Le bourgeon principal, à gauche de la cardioïde, lui est attaché au point c = –3/4. Il s'agit d'un disque centré en c = –1 et de rayon 1/4. Il s'agit de l'ensemble des points paramètres qui, à la limite, convergent vers un cycle de période 2.
- Les autres bourgeons tangents à la cardioïde sont les points admettant d'autres périodicités. Chacun de ces bourgeons est appelé « bourgeon p/q ». Il s'agit de l'ensemble des points paramètres convergeant vers un cycle de période q.
- Enfin, chaque bourgeon porte lui-même des bourgeons, représentatifs d'une périodicité différente, selon le même schéma.
Variantes
L'ensemble de Mandelbrot peut être généralisé pour des puissances d supérieures à 2 : \(z_n+1=z_n^d+c\). Ces généralisations sont parfois appelées « multibrot ».
Exemples : Source des images



Il est aussi possible de généraliser encore, et de considérer plutôt des itérations quelconques de la forme :
\(z_n+1=f(z_n,c)\)