Dimension - Images Fractales

Préambule

La dimension d'une fractale D est une grandeur qui traduit la façon dont une fractale occupe l'espace. La dimension d'une fractale n'est pas une chose simple à calculer. A l'inverse d'un droite, d'un plan et d'un volume qui ont une dimension entière ; une fractale a comme dimension un réel positif. La dimension fractale est un terme qui recouvre plusieurs définitions. Les définitions les plus importantes sont la dimension de Hausdorff, la dimension de Minkowski-Bouligand et la dimension de corrélation

Approche didactique

La dimension D d'un segment, d'un cercle et d'une courbe régulière est de 1. Sa longueur est multipliée par $ 2^{1}=2 $ lorsque sa taille double.
La dimension D d'une surface simple et bornée est de 2. Elle a une aire finie et cette aire est multipliée par $ 2^{2}=4 $ lorsque sa taille double.
La dimension D d'un volume simple et borné dans l'espace est de 3. Il a un volume fini et ce volume est multiplié par $ 2^{3}=8 $ lorsque sa taille double.

Soit D la dimension d'un objet, alors la mesure de cet objet est multipliée par $n^{D}$ lorsque la taille de cet objet est multipliée par n.

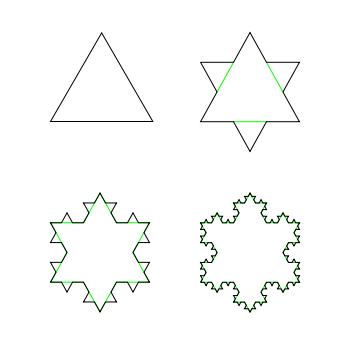
Or, par exemple, la longueur de la courbe de Koch est multipliée par 4 lorsque sa taille triple (En effet, cette courbe est précisément définie comme étant constituée de quatre copies d'elle-même, trois fois plus petites). Puisque $ 4 \approx 3^{1,26} $ , on peut considérer intuitivement qu'il s'agit d'un objet de dimension : $D \approx 1,26$ (plus précisément, $ D = {log ⁡4 \over log3} $ ). Il ne s'agit plus d'une simple courbe unidimensionnelle, ni d'une surface, elle se situe « entre les deux ». Cette « dimension fractale », non entière, est caractéristique des ensembles fractals.

Quand la fractale est formée de répliques d'elle-même en plus petit, sa dimension fractale peut se calculer comme suit :

$D={{log(n)} \over {log(h)}}$ où n réprésente le nombre de motifs répétés et h le facteur de réduction

$Evolution fractale$

La source de l'image

Exemple

La source clickable

Un côté du flocon de Koch est formé de n = 4 exemplaires de lui-même réduit d'un facteur h = 3. Sa dimension fractale vaut :

$$ D={{ln(4)} \over {ln(3)}} \approx 1,2618595\ldots $$

le triangle de Sierpinski est formé de n = 3 exemplaires de lui-même réduit d'un facteur h = 2. Sa dimension fractale vaut :

$$ D={{ln(3)} \over {ln(2)}} \approx 1,5849625\ldots $$

le tapis de Sierpinski est formé de n = 8 exemplaires de lui-même réduit d'un facteur h = 3. Sa dimension fractale vaut :

$$ D={{ln(8)} \over {ln(3)}} \approx 1,892789\ldots $$

Tableau des dimensions

Définition	Applicabilité	Formule	Commentaires
Dimension de Hausdorff	La plus rigoureuse, et définie pour tout ensemble, elle est peu aisée à mettre en œuvre.	$ D_{H}=inf \{ s,H^{8}(X)=0 \} = sup \{ s,H^{8}(X)= \infty \} $ où $ H^{8}(X) $ est la mesure de Hausdorff de l'ensemble	Elle s'appuie sur une mesure, la mesure de Hausdorff. C'est la valeur critique de s pour laquelle la valeur de la mesure $ H^{8}(X) $ passe de 0 à l'infini.
Dimension d'homotétie (1)	Limitée aux ensembles à homothéties internes	$ D_{H} $ est solution de $$ \sum_{k=1}^N r_{k}^{D_{h}}=1 $$ où N est le nombre d'homothéties et $ r_{k} $ le rapport l'homothétie de rang k. Dans le cas de rapports identiques, elle admet une solution analytique simple (voir ci-dessous)	C'est la traduction la plus simple de la dimension de Hausdorff, applicable aux seuls ensembles fractals à homothétie interne où les homothéties qui les composent sont toutes deux à deux disjointes.
Dimension d'homotétie (2)	Limitée aux ensembles à homothéties internes de même rapport	$ D_{h}={{ln(N)} \over {ln({1 \over {r}})}} $où $N$ est le nombre d'homothéties et $ r^{k} $ le rapport d'homothétie	C'est un cas particulier de solution pour l'équation générale ci-dessus. La dimension d'homothétie vaut alors le quotient logarithmique entre le nombre d'homothéties internes de l'ensemble, sur l'inverse du rapport d'homothétie.
Dimension de Minkowski-Bouligand ou 'Box-counting'	Tout ensemble	$$ D_{box}=\lim_{\varepsilon \to 0} {log N (\varepsilon) \over log({1 \over \varepsilon})} $$ où $N(ε)$ est un nombre de sous-ensembles de diamètre au plus $ε$ nécessaires pour recouvrir l'ensemble.	La plus courante et la plus simple pour mesurer numériquement la dimension d'une fractale. Elle prend pour base la couverture de l'ensemble fractal par des ensembles de taille décroissantes. S'appuie sur une notion de comptage et non de mesure, ce qui la rend moins universelle.

Evolution du tapis de Sierpinski

Définition	Applicabilité	Formule	Commentaires
Dimension de Hausdorff	La plus rigoureuse, et définie pour tout ensemble, elle est peu aisée à mettre en œuvre.	\( D_{H}=inf \{ s,H^{8}(X)=0 \} = sup \{ s,H^{8}(X)= \infty \} \) où \( H^{8}(X) \) est la mesure de Hausdorff de l'ensemble	Elle s'appuie sur une mesure, la mesure de Hausdorff. C'est la valeur critique de s pour laquelle la valeur de la mesure \( H^{8}(X) \) passe de 0 à l'infini.
Dimension d'homotétie (1)	Limitée aux ensembles à homothéties internes	\( D_{H} \) est solution de $$ \sum_{k=1}^N r_{k}^{D_{h}}=1 $$ où N est le nombre d'homothéties et \( r_{k} \) le rapport l'homothétie de rang k. Dans le cas de rapports identiques, elle admet une solution analytique simple (voir ci-dessous)	C'est la traduction la plus simple de la dimension de Hausdorff, applicable aux seuls ensembles fractals à homothétie interne où les homothéties qui les composent sont toutes deux à deux disjointes.
Dimension d'homotétie (2)	Limitée aux ensembles à homothéties internes de même rapport	\( D_{h}={{ln(N)} \over {ln({1 \over {r}})}} \)où \(N\) est le nombre d'homothéties et \( r^{k} \) le rapport d'homothétie	C'est un cas particulier de solution pour l'équation générale ci-dessus. La dimension d'homothétie vaut alors le quotient logarithmique entre le nombre d'homothéties internes de l'ensemble, sur l'inverse du rapport d'homothétie.
Dimension de Minkowski-Bouligand ou 'Box-counting'	Tout ensemble	$$ D_{box}=\lim_{\varepsilon \to 0} {log N (\varepsilon) \over log({1 \over \varepsilon})} $$ où \(N(ε)\) est un nombre de sous-ensembles de diamètre au plus \(ε\) nécessaires pour recouvrir l'ensemble.	La plus courante et la plus simple pour mesurer numériquement la dimension d'une fractale. Elle prend pour base la couverture de l'ensemble fractal par des ensembles de taille décroissantes. S'appuie sur une notion de comptage et non de mesure, ce qui la rend moins universelle.